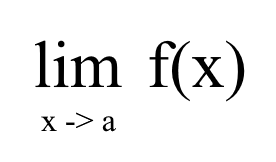Day 4 - Calculus (Limit)

Introduction

Today, we’re going to review the fundamentals of chain rule. Let’s just get on with it.

Example Question

Let’s say we have a question with this equation :

\[f(x) = (3x^2 + 5x - 7)^4\]

Other than the usual chain rule formula, we can use this other form to solve it which is more simple to understand :

\[\frac{dy}{dx} = \frac{dy}{da} \cdot \frac{da}{dx}\]

First of all, what even is the dy or dx? What does the d even mean. Let’s use dy/dx as an example. This basically means the derivative of y with respect to x. Remember that f(x) is basically just y in math. Then, what in the world is da. Well, first we have to explain the process of solving the question.

Step 1 : Assumption

First, if we ever have a question where an entire function inside some parantheses has an exponent, we have to assume that the function iside the parantheses is some random letter (let’s say a). So, the question from before should look like this.

\[a = 3x^2 + 5x - 7\] \[f(x) = (a)^4\]

Step 2 : Derivative the f(x) and the a

Next, the dy/da part in the formula means that we have to find the derivative of y (f(x)) to the respect of a. We can just use this formula to solve it easier :

\[f'(x) = n x^{n-1}\]

So, the answer will be :

\[\frac{dy}{da} = 4{a}^{3}\]

Next, we’ll find the derivative of the a, which is defined from the formula as da/dx :

\[\frac{da}{dx} = 6x + 5\]

Step 3 : Multiple both of them

Next, all we have to do is multiply both of the dy/da and da/dx and replace the a back with its original equation, which should be :

\[\frac{dy}{dx} = \frac{dy}{da} \cdot \frac{da}{dx}\] \[\frac{dy}{dx} = 6x + 5 \cdot 4{a}^3\] \[\frac{dy}{dx} = 4 \cdot (6x + 5) \cdot ({3x^2 + 5x - 7})^3\]

And we’re done!