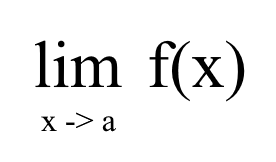Day 3 - Calculus (Limit)

Introduction

For today, we’re going to learn about random methods to solve derivatives. I got no introduction, let’s just move on man.

Random Fact!

When solving a derivative question, if we want to find a specific x on the derivative and the answer is larger than 0 (x > 0), that means the graph is going up on that x. If it’s smaller than 0 (x < 0), it’s the opposite. This will be useful in finding the peak or the minimum is for the derivative.

Binomial Theorem

What’s a Binomial Theorem? It’s a way to ease huge exponent operations, such as (x+y)^4 or larger. It’s defined by this formula :

\[(a + b)^n = \sum_{k=0}^{n} \binom{n}{k} a^{n-k} b^k\]

The gist of it is basically that we have to find each variable’s coefficients and exponents starting from whatever exponent n we have. We can find the coefficients using the factorial (n k), which is defined as this :

\[\binom{n}{k} = \frac{n!}{k!(n-k)!}\]

If we had to find one that has an exponent of 4, it will find the constant for each variable using this formula. The k starts from 0 and keeps going up until it reaches that exponent (4). After that, we have this :

\[a^{n-k} b^k\]

We use the n and k from before to determine the variable’s exponent. Pretty straightforward.

Chain Rule

The chain rule is used for derivatives with large exponents, such as (3x-7)^12. The formula is defined as:

\[\frac{d}{dx} [f(g(x))] = f'(g(x)) \cdot g'(x)\]

Let’s use the example question :

\[y = (3x - 7)^{12}\]

First we use the power rule that is used for other derivatives where the exponent goes to the left side and the original exponent gets decremented by 1 :

\[\frac{d}{dx} (3x - 7)^{12} = 12(3x - 7)^{11}\]

Next, we find the derivative of the operation inside the brackets :

\[\frac{d}{dx} (3x - 7) = 3\]

Now just multiply everything like this :

\[\frac{d}{dx} (3x - 7)^{12} = 12(3x - 7)^{11} \cdot 3\] \[= 36(3x - 7)^{11}\]

This method works for any function with the form (x + y)^n!