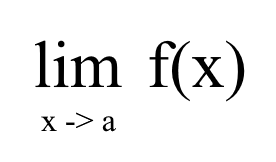Day 2 - Calculus (Limit)

Introduction

Before, we explain that some limit operations can result in a 0 divided by 0 so we have to resort to finding the limit using graphs. Here, we will discuss other ways to find the limit without looking at graphs all day. There are 3 ways to do this, which is…

Direct Substitution

In Direct Substitution, all we have to do is well… substitute the value of whatever variable we have to the function directly. Here is an example!

\[\lim\limits_{x \to 1} (2x - 1)\]

The x here reaches the value of 1, so we can just substitute that right to the function in the left, which results in (2 x 1-1) = 1. This doesn’t apply to every limit operation though, especially if it results in a 0/0. If this happens, we have to resort to other methods, such as…

Factoring

Some limit operations has functions in fractions (x/y). And as I’ve previously explained in my previous post, some can result in a 0/0. A possible solution is to factore the numerator/denominator (if applicable). Think of it as breaking down the function into smaller pieces. An example is :

\[\lim\limits_{x \to 1} \frac{x^2 - 1}{x-1}\]

If we directly substitute 1 into the function, it will always result in a 0/0. But… we can see that the numerator (x^1 - 1) can be further broken down with the formulas below

Factoring Formulas

From the rules above, we can get that (x^1 - 1) can be broken down to (x-1) (x+1) / (x-1). We can see that there are 2 (x-1)’s in the fraction, so we can just cross/delete them out and then the result will be :

\[\lim\limits_{x \to 1} \frac{(x+1)(x-1)}{x-1}\] \[\lim\limits_{x \to 1} \frac{(x+1)\cancel{(x-1)}}{\cancel{x-1}}\] \[\lim\limits_{x \to 1} (x+1)\]

Now, we can directly substitute 1 into the function, which will result in 2. There is another way other than factoring which is significantly harder depending on which formula you use. Introducing, derivatives!

Derivatives

Derivatives are basically where we try to measure the difference between spots. Do they go higher or lower or something else? There are 2 ways that I’m personally used to, which is the definitive way and the easy way. The definitive formula is as such :

\[f'(x) = \lim\limits_{h \to 0} \frac{f(x+h) - f(x)}{h}\]

Unfortunately, I refuse to explain the definitive way because it is going to take way too long so I’ll just revert to the easy way, which is :

\[f'(x) = n x^{n-1}\]

From this formula, we can differentiate a function easily. Let’s apply this to an example:

\[\lim\limits_{x \to 1} 2x^2\] \[f'(x) = 2*2x^2-1\] \[f'(x) = 4x^1\]

Now, we can use the x from the limit :

\[\lim\limits_{x \to 1} 4x^1\] \[\lim\limits_{x \to 1} 4*1^1 = 4\]

Conclusion

We explored three main ways to solve limits:

1. Direct Substitution – The easiest method if it doesn’t lead to 0/0.
2. Factoring – Useful when the function can be broken down.
3. Derivatives – If the other two fails.

Understanding these techniques will help solve limits efficiently without relying on graphs all the time. Happy learning!