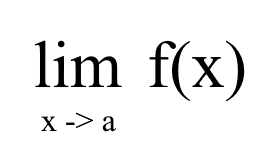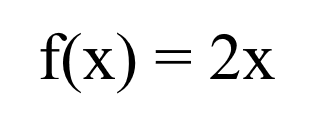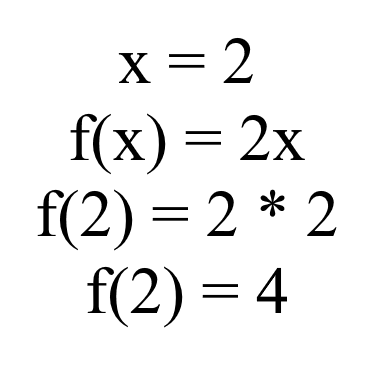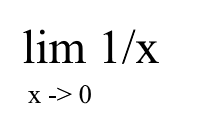Day 1 - Calculus (Limit)
Introduction to Calculus.
Introduction
In my first day of Calculus, well… we didn’t actually start learning calculus yet, but a review of past material in high school. The topic we reviewed today was Limits. Before we explain what a limit is or even how it works, we have to go back again to Functions (in Mathematics), not functions in coding terms.
What’s a Function?
A simple function formula
In very oversimplified terms, a function is basically where we substitute/transfer the value of x in f(x) into the right side (which is 2x in the picture above). The set of possible inputs (aka values of x in the example) is called the domain, and the set of possible outputs (results) is called the codomain.
Example Question
The value of x we have is 2, then we substitute that value into the codomain’s x, which will result in f(2) = 2 * 2. Then we just multiply the numbers in the right side and we’ll get 4-Pretty straightforward. But Limit though… it’s a bit trickier than just substituting x’s.
How does Limit work?
Limit’s fundamental theory is basically either trying to reach a certain point or a certain point where you can’t go any further beyond that point. Let’s take an example below :
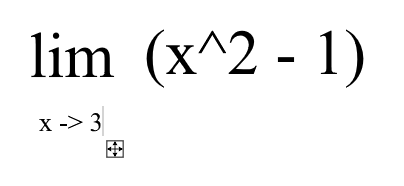Limit of x = 3 in f(x) = x^2-1
The example above wants to find what’s the limit aka what point it meets when x gets closer to 3. We can just substitute x inside the function with 3 and then get 3^2 - 1, which is 8. But… there is also the possibility of one of the answers being either infinite or not defined. These possibilities can happen when a 0 is usually involved, such as the example below :
Limit of x = 0 in f(x) = 1/x
If we try to substitute 0 in the function, it will result with 1/0. Wait a minute, nothing divided by 0 can result in a 1, which means it is not defined. How are we supposed to know what the actual limit value is? Well… if we try to place the function inside a graphic calculator, it would look like this.
Graphic Calculator of f(x) = 1/x in geogebra.org
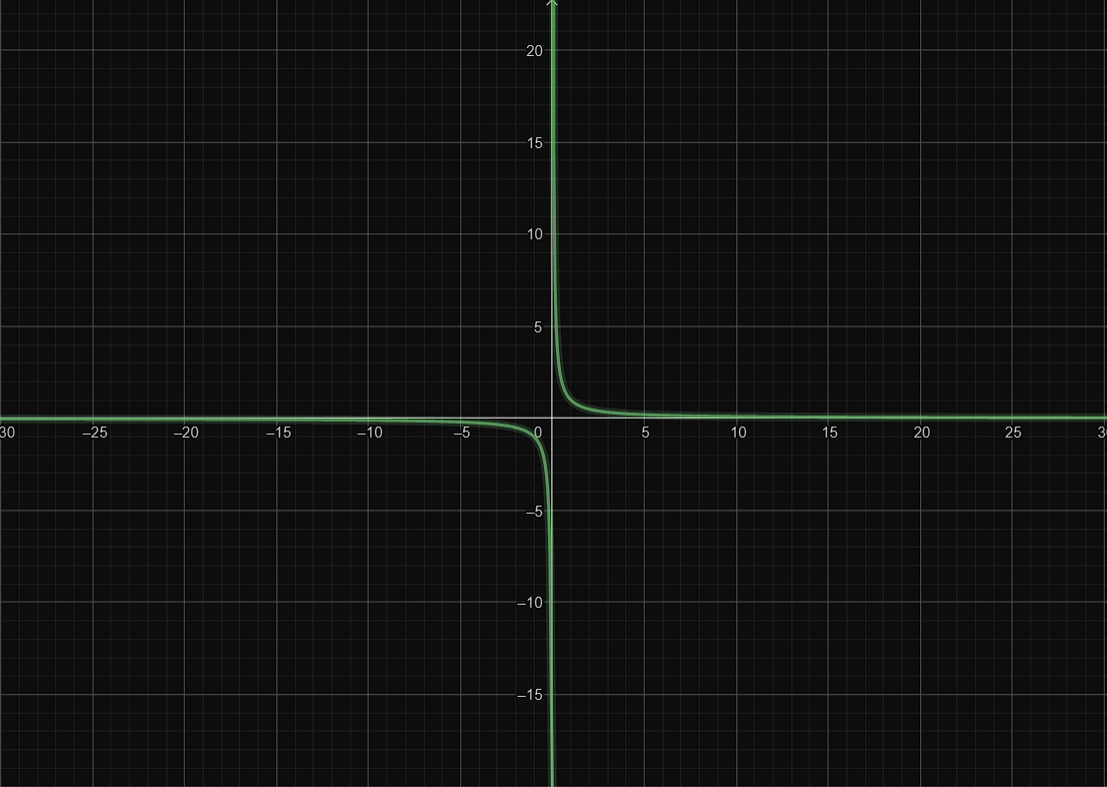
In the picture above, we can see in the positive side (top right) that the higher the value of x, the lower the y but it will never reach 0, which is the x that we want to find the limit for. Same case with the negative side (bottom left). To find a limit at x = 0, the positive side (numbers after 0) and negative side (numbers below 0) has to meet at some point, but we can see that the number gets larger to infinity in the positive side, and smaller to negative infinity in the negative side. Thus, we can deduce that the limit doesn’t exist at all. That’s why sometimes we need to see the results from both sides (positive and negative) instead of blindly substituting x’s.
Conclusion
Limits are basically where the positive side (numbers after x) and the negative side (numbers below x) meet. Sometimes it could have a result, or simply have no result at all. If I’m wrong, feel free to give a feedback on why I’m wrong. Thank you for reading my post!