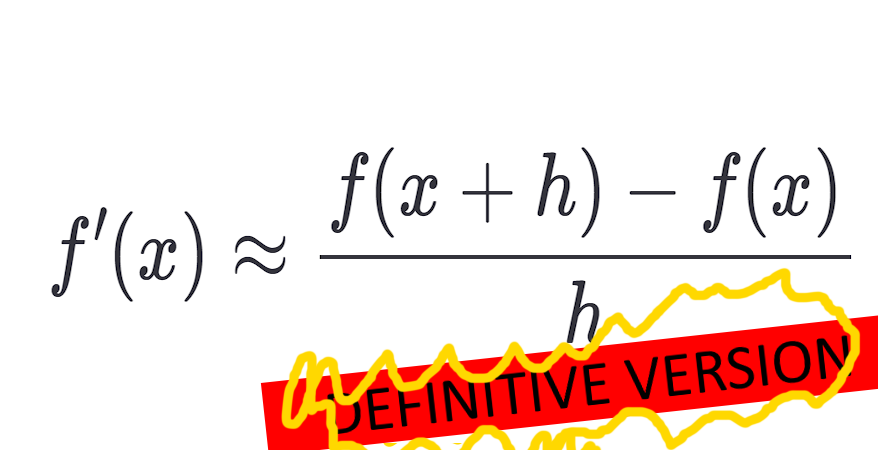Numerical Derivatives in a nutshell (Calculus Material 6)
Where the heck did the function go?
Introduction
Alright this is getting a bit tricky. Imagine a regular function. When we’re talking derivatives, you’d probably want to find the derivative of that function, right? But… what if there’s no function at all? What if you were just given a few x points and the values of those x points in a table and you had to figure it out yourself? That’s where Numerical Derivatives comes in.
Numerical Derivatives
There are three common methods for approximating derivatives numerically, based on values of a function \(f(x)\) at various points:
1. Forward Difference
\[f'(x) \approx \frac{f(x + h) - f(x)}{h}\]You’re looking ahead, calculating the slope between the current point and the next one. It’s easy, but not the most accurate. Still good when you can’t look back. Like life. Or your past mistakes. Haiyaa…
2. Backward Difference
\[f'(x) \approx \frac{f(x) - f(x - h)}{h}\]This one looks behind. It’s useful when you only know previous values. You know, when you’re stuck in the past and can’t move on… haiyaa…
3. Central Difference
\[f'(x) \approx \frac{f(x + h) - f(x - h)}{2h}\]This is the best of both worlds. It takes the average of forward and backward differences. It’s more accurate, assuming you’re not too close to the edge of your data.
Example
Let’s say you have this table of values:
| \(x\) | \(f(x)\) |
|---|---|
| 1.0 | 2.718 |
| 1.1 | 3.004 |
| 1.2 | 3.320 |
Let’s try a central difference at \(x = 1.1\). That means we have to use the x points before and after \(x = 1.1\), which is \(1.0\) and \(1.2\):
\[f'(1.1) \approx \frac{f(1.2) - f(1.0)}{2 \times 0.1} = \frac{3.320 - 2.718}{0.2} = 3.01\]So yeah, that’s your estimated slope. Is it perfect? No. Is it good enough? Absolutely. If we were to use forward difference, we would only use \(1.1\) and \(1.2\), while backwards difference would use \(1.1\) and \(1.0\).
Conclusion
Numerical Derivatives are the go-to when life refuses to give you a proper function. Just some scattered points and a prayer. And that’s okay. You’re not expected to be perfect. You just have to be close enough.