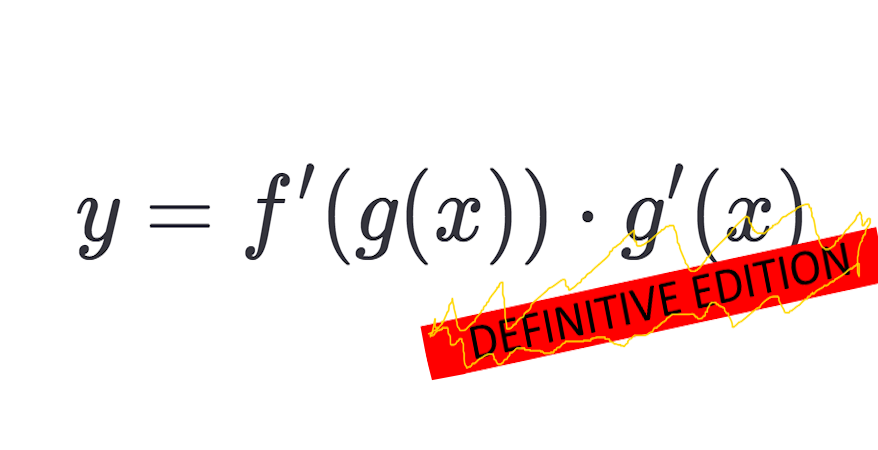Chain Rule in a nutshell (Calculus Material 3)

Introduction

What happens when a function inside a function needs to be derivatived? Get derivatived? Is that even a word? You know what I mean. Well, there’s a solution for that. Introducing Chain Rule

Chain Rule

The chain rule is used for derivatives with large exponents or a function inside a function, such as (3x-7)^12. The formula is defined as:

\[\frac{d}{dx} [f(g(x))] = f'(g(x)) \cdot g'(x)\]

Let’s use the example question :

\[y = (3x - 7)^{12}\]

First we use the power rule that is used for other derivatives where the exponent goes to the left side and the original exponent gets decremented by 1 :

\[\frac{d}{dx} (3x - 7)^{12} = 12(3x - 7)^{11}\]

Next, we find the derivative of the operation inside the brackets :

\[\frac{d}{dx} (3x - 7) = 3\]

Now just multiply the already decremented exponent function with the derivative of the operation inside the brackets like this :

\[\frac{d}{dx} (3x - 7)^{12} = 12(3x - 7)^{11} \cdot 3\] \[= 36(3x - 7)^{11}\]

And we’re done! This method works for any function with the form (x + y)^n!

Conclusion

The Chain Rule helps us take derivatives of composite functions—that is, functions inside functions. By multiplying the derivative of the outer function (with the inner untouched) by the derivative of the inside, we can simplify even the scariest expressions.

Just remember:

1. Use the power rule on the outside first.
2. Then multiply by the derivative of the inside.