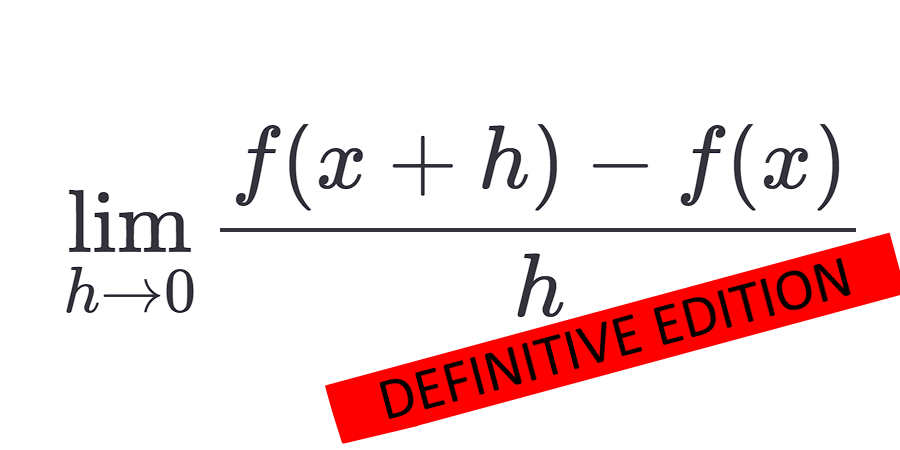Derivatives in a nutshell (Calculus Material 2)
Another way to solve Limits.
Introduction
Remember how I said in the previous post there are 3 other ways to solve limits? The third way is to use derivatives, which is a whole other can of worms in terms of material and content. That’s why it needs a seperate post instead of being clumped together in the limit post. Let’s get on with it shall we?
What are Derivatives?
Derivatives are basically where we try to measure the difference between spots. Do they go higher or lower or something else? There are 2 ways that I’m personally used to, which is the definitive way and the easy way. Let’s explain the easy way first, since it’s pretty much a shortcut that is easily understandable compared to the definitive way.
Easy Way
\[f'(x) = n*x^{n-1}\]What’s a n? The n here is basically the exponent in the function. Let’s say we have a function of x^2. The n here would be 2. Let’s apply this to an example like below:
Example:
\[\lim\limits_{x \to 1} 2x^2\]From the function above, the n would be 2. Now all we have to do is multiply the same function with that n and reduce the exponent n by 1 like below.
\[f'(x) = 2 \cdot 2x^{2 - 1}\] \[f'(x) = 4x^1\]Now, we can finally use the x from the limit :
\[f'(1) = 4 * 1 = 4\]Definitive Way
The definitive formula is as such :
\[f'(x) = \lim\limits_{h \to 0} \frac{f(x+h) - f(x)}{h}\]It means: “Find how much the function changes when x changes by a very tiny amount (h), and see what value that change approaches as h gets super close to 0.”
Example:
Let’s say:
\[f(x) = x^2\]Then, we just have to replace the f(x) in the formula with the function in our example, and the f(x+h) in the formula to our function if (x+h) is substituted into it like below :
\[f'(x) = \lim\limits_{h \to 0} \frac{(x + h)^2 - x^2}{h}\]Next, expand the top part of the fraction:
\[f'(x) = \lim\limits_{h \to 0} \frac{x^2 + 2xh + h^2 - x^2}{h}\]Remove the x^2:
\[f'(x) = \lim\limits_{h \to 0} \frac{2xh + h^2}{h}\]Factor out h:
\[f'(x) = \lim\limits_{h \to 0} (2x + h)\]Cancel out the h because h is to 0:
\[f'(x) = 2x\]Now we have the derivative. Pretty complicated honestly.
Random Fact!
When solving a derivative question, if we want to find a specific x on the derivative and the answer is larger than 0 (x > 0), that means the graph is going up on that x. If it’s smaller than 0 (x < 0), it’s the opposite. This will be useful in finding if the graph has a top peak or the minimum (bottom peak) for the derivative.
Comparison of Limit Solving Methods
| Method | When to Use | Example Problem |
|---|---|---|
| Direct Substitution | When plugging in the value doesn’t cause an error | lim as x→2 of (x + 1) = 3 |
| Factoring | When substitution gives 0/0 and the expression can be factored | lim as x→1 of (x² - 1)/(x - 1) = 2 |
| Derivatives | When it’s 0/0 and factoring fails or is hard (use L’Hôpital’s Rule) | lim as x→0 of sin(x)/x = 1 |
Conclusion
We explored 2 ways to solve limits with derivatives, which are :
- Easy Way - Easily understandable. Use this if you’re lazy
- Definitive Way - More complex but as the name says, it’s the more definitive way. Use this if explicitly mentioned in a question.
Understanding these techniques will help solve limits efficiently without relying on graphs all the time. Happy learning!